2477. Minimum Fuel Cost to Report to the Capital
Medium
There is a tree (i.e., a connected, undirected graph with no cycles) structure country network consisting of n cities numbered from 0 to n - 1 and exactly n - 1 roads. The capital city is city 0. You are given a 2D integer array roads where roads[i] = [ai, bi] denotes that there exists a bidirectional road connecting cities ai and bi.
There is a meeting for the representatives of each city. The meeting is in the capital city.
There is a car in each city. You are given an integer seats that indicates the number of seats in each car.
A representative can use the car in their city to travel or change the car and ride with another representative. The cost of traveling between two cities is one liter of fuel.
Return the minimum number of liters of fuel to reach the capital city.
Example 1:
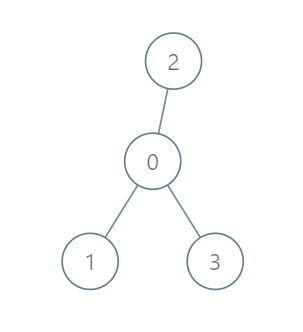
Input: roads = [[0,1],[0,2],[0,3]], seats = 5
Output: 3
Explanation:
- Representative1 goes directly to the capital with 1 liter of fuel.
- Representative2 goes directly to the capital with 1 liter of fuel.
- Representative3 goes directly to the capital with 1 liter of fuel.
It costs 3 liters of fuel at minimum.
It can be proven that 3 is the minimum number of liters of fuel needed.
Example 2:
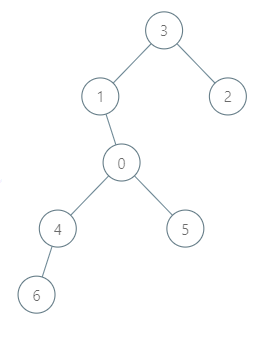
Input: roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]], seats = 2
Output: 7
Explanation:
- Representative2 goes directly to city 3 with 1 liter of fuel.
- Representative2 and representative3 go together to city 1 with 1 liter of fuel.
- Representative2 and representative3 go together to the capital with 1 liter of fuel.
- Representative1 goes directly to the capital with 1 liter of fuel.
- Representative5 goes directly to the capital with 1 liter of fuel.
- Representative6 goes directly to city 4 with 1 liter of fuel.
- Representative4 and representative6 go together to the capital with 1 liter of fuel.
It costs 7 liters of fuel at minimum.
It can be proven that 7 is the minimum number of liters of fuel needed.
Example 3:

Input: roads = [], seats = 1
Output: 0
Explanation: No representatives need to travel to the capital city.
Constraints:
- 1 <= n <= 105
- roads.length == n - 1
- roads[i].length == 2
- 0 <= ai, bi < n
- ai != bi
- roads represents a valid tree.
- 1 <= seats <= 105
문제 풀이
- 그래프가 하나 주어지며 이 그래프는 0부터 n - 1 까지 주어진다.
- 그래프의 간선들이 리스트로 주어지고 자동차에 탈 수 있는 총인원의 수가 주어진다.
- 0이 목적지이며 각각의 숫자에서 자동차를 타고 다른 노드로 이동할때마다 1의 기름값이 사용된다.
- 여기서 기름값이 최소로 드는 값을 구해야한다.
- 자동차에 탈 수 있는 총인원의 수는 현재노드에서 다음노드로 이동시에 이전 노드에서 넘어온 사람을 그 숫자만큼 태우고 이동할 수 있다.
- 즉, 노드가 3개가 연결되어있고 총인원 수가 3이라면 맨 마지막에서 이동 후 한사람을 태우고 그 다음 노드에서 한사람을 태우면 각각 노드에서의 이동 기름값인 1 + 1 + 1만 소비된다.
- 문제 제한을 보면 10^5이며, N^2의 시간복잡도로는 풀 수 없다.
- 노드를 각각 한번씩만 들리고 문제를 풀 수 있다면 DFS, BFS도 가능할 것이다.
- DFS로 접근해보자, 가장 중요한 포인트는 노드를 이동할때 마다 각 노드에서 출발하는 사람의 수를 중첩하여 더 해주어야한다.
- 그리고 나머지 연산을 이용하여 0으로 나누어 떨어지지 않으면 한 사람의 값만 추가하여 정답에 더 해야한다.
- 그 이유는 총 인원보다 적을때 그 그룹은 어쨋거나 한 자동차내에 탑승할 수 있기 때문이다.
- 마지막 노드까지 탐색한 후에 노드의 개수를 리턴해주며 더해줘야 하며, 정답을 처리할때는 차에 탑승 가능한 총 인원수와 노드에서 나온 중첩된 인원수를 사용한다.
- 즉 차에 수용가능한 인원수로 현재 중첩된 인원들을 나누어 몫은 바로 노드를 이동하는 소요시간으로 더해질것이다.
- 그리고 위에서 언급한 나머지 연산을 통해 한 그룹을 추가할지를 정한다.
- 마지막으로 현재 노드가 0인 노드에 도착하지 않았을때 값들을 정답에 더해줘야한다.
- 왜냐하면 post order, 즉 후위순회로 노드의 연료 계산이 적용되기 때문에 0에 도착했을 당시의 연료 소비는 없는 것이다.
소스 코드
class Solution:
def __init__(self):
# global answer
self.ans = 0
def dfs(self, curr, seats, visited, graph):
# initiate person count
cnt = 1
for nxt in graph[curr]:
if nxt not in visited:
visited.add(curr)
cnt += self.dfs(nxt, seats, visited, graph)
# how many cars are from here?
tmp = cnt // seats
# over 0 means one more car is necessary
if cnt % seats != 0:
tmp += 1
# Cause post order
if curr != 0:
self.ans += tmp
return cnt
def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:
graph = defaultdict(list)
visited = set()
for a, b in roads:
graph[a].append(b)
graph[b].append(a)
self.dfs(0, seats, visited, graph)
return self.ans'컴퓨터공학 > LeetCode 1000' 카테고리의 다른 글
| [LeetCode] 280. Wiggle Sort (0) | 2023.02.14 |
|---|---|
| [LeetCode] 1523. Count Odd Numbers in an Interval Range (0) | 2023.02.14 |
| [LeetCode] 567. Permutation in String (0) | 2023.02.10 |
| [LeetCode] 6. Zigzag Conversion (1) | 2023.02.04 |
| [LeetCode] 1056. Confusing Number (0) | 2023.01.02 |
![[LeetCode] 2477. Minimum Fuel Cost to Report to the Capital](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FdbiNgY%2FbtrYUv8FfN6%2FTsjC9KocEnKhmOjqJBTEF1%2Fimg.png)