Chapter 5. Clustering - 02

Cluto : Clustering Toolkit - Clustering Library [Seven different criterion fuctions]

Internal clustering quality

Main 특징

1. 특정한 클러스터링 표준 함수를 최적화하는 방법을 찾는다.
2. 각각의 클러스터(객체 그리고 특징들)를 가장 잘 설명하고 차별화(관계를) 하는 것을 나타낸다.
3. 시각화, 흩어짐 조절.

partiional, agglomerative, graph-partitioning 클러스터링 알고리즘을 제공한다.
partitional 그리고 agglomerative 클러스터링 알고리즘인 7개의 다른 표준 함수들을 제공한다.
* Traditional local criteria 을 몇몇 제공한다.

vcluster : 객체의 특징과 관련하여 작동
scluster : 객체의 유사도와 관련하여 작동

 

K means 클러스터링에서 적절한 K ?

다른 K를 찾을때, 중심으로부터 평균 거리의 변화를 비교한다.
평균적으로 적절한 K를 찾고 난 이후부터 변화가 적어진다.
즉, 중심으로 부터 거리의 평균의 감소가 적다. 

K = 3 일때부터 Sum of squared error 가 줄어드는 그래프의 기울기가 작다.

 

Sum of Squared Error? 

오차 제곱합이란, 이전 Centroid(중심 값)들과 클러스터에 속해진 지점들의 평균 중심값이 얼마나 차이나는지를 
의마한다. 또한, 클러스터안의 데이터들이 모여있을때, 각각의 데이터들이 중심과의 거리가 작을 수록 더 좋다.
이말은, SSE를 최소화 했을때 좋은 클러스터 형태를 나타내는 것이다.

K-means / K를 구하는 과정

1. K개의 Centroid (중심 좌표) 를 임의로 정한다.
2. K 개의 임의의 좌표가 설정된다.
3. 모든 좌표의 거리를 각 K개의 Centroid 들과 계산하여 가장 거리가 짧은 곳을 찾는다.
4. 3번에서 결정된 Centroid 데이터 셋에 좌표들을 넣는다.
5. K 개의 클러스터에 모인 좌표들을 계산하여 중심점 Centroid 를 찾는다. ( 모든 좌표들의 mean 값을 찾자. )
6. 이전 중심점이 클러스터링 된 값들의 중심 값과 차이를 비교하여 Sum of Squared Error가 0이 될때까지 3 번부터 5번의 과정을 반복한다.
7. SSE가 0이라면 더 이상 중심점을 찾을 필요가 없다.

 

Hierarchical Clustering 계층적 군집화

https://www.displayr.com/what-is-hierarchical-clustering/

계층적 클러스터링을 얻기 위한 두가지 중요 방법

1. Agglomerative : 각각의 클러스터들로 부터 시작하여, 각 단계마다 단 하나의 클러스터가 남을때까지 가까운 클러스터들을 병합한다.
2. Divisive : 관련된 모든 클러스터를 시작으로, 각 단계마다 클러스터들을 쪼개면서 진행한다.

특징

• 특정한 클러스터들의 개수를 정할 필요가 없다.
• 적절한 레벨에서 클러스터들의 숫자를 잘라 개수를 정할 수 있다.
• 생물과학등과 같은 분야에서 클러스터링을 하기에 적당한 의미를 담을 수 있다.

* 그외 : 전통적인 계층적 알고리즘들은 유사도나 메트릭스간의 거리를 활용하여 병합하거나 나눈다.

 

클러스터링 알고리즘

Agglomerative

https://www.geeksforgeeks.org/hierarchical-clustering-in-data-mining/

1. 메트릭스의 거리를 계산한다.
2. 각 데이터들을 클러스터로 만든다. 
3. 가장 가까운 클러스터들을 병합한다.
4. 매트릭스의 거리들을 업데이트한다.
5. 하나의 클러스터가 남을때거나, K개의 클러스터들이 남을때까지 3, 4번을 반복한다.

* 클러스터들의 거리를 계산할때가 가장 중요한 동작이다.

 

Divisive Clustering

https://www.geeksforgeeks.org/hierarchical-clustering-in-data-mining/

 

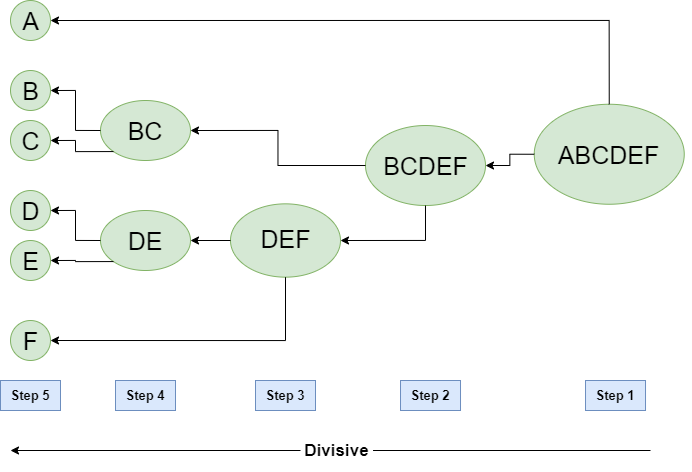
클러스터들의 각각의 거리 책정

 

최소 거리 Mininum Distance(Single link)

https://www.datacamp.com/community/tutorials/hierarchical-clustering-R

각기 다른 클러스터들안에서 가장 가까운 좌표들을 기반으로 두개의 클러스터들의 거리를 측정한다.

장점 : 타원형이 아닌 모양의 클러스터들을 나누기 쉽다.
단점 : 잡음(Noise) 이나 이상치(Outlier)에 민감하다.

 

최대 거리 Maximum distance(Complete link)

https://www.datacamp.com/community/tutorials/hierarchical-clustering-R

각기 다른 클러스터들안에서 가장 먼 좌표들을 기반으로 거리를 측정한다.

장점 : 잡음(Noise) 이나 이상치(Outlier)에 강하다.
단점 : 큰 클러스터들을 망가뜨리는 경향이 있다.
원형의 클러스터들에 치우쳐진다.

평균 거리 Average Distance(UPGMA)

두개의 클러스터들안에서 짝이 이루어진 좌표들의 평균을 이용하여 거리를 측정한다. 또한 확장성을 위한 평균 연결의 사용을 필요한다.

 

그룹 평균 Group Average

https://www.datacamp.com/community/tutorials/hierarchical-clustering-R

Single link와 Complete link의 중간으로, 잡음(Noise)와 이상치(Outlier)들에 대한 취약함이 적다. 하지만 원형의 클러스터들에 편향된다.

 

Ward's Method 

https://jbhender.github.io/Stats506/F18/GP/Group10.html

두개의 클러스터를 병합했을때 Squared error가 증가하는 것을 기반으로 클러스터링한다. 비슷한 그룹 클러스터들이 발생한다.

특징

잡음(Noise)과 이상치(Outlier)과 관련된 취약함이 적다.
하지만 구형 클러스터들에 치우쳐져 있다.
K-means로 초기화 하여 사용할 수 있다. (Sum of Squared Error)

 

Minimum Spanning Tree : Agglomerative Hierarchical Clustering의 하나이다.

특징

어느 좌표나 가능하며, 트리 자료구조로 이루어지면서 시작한다.
가장 가까운 포인트를 찾는다. 포인트들을 연결하면서 트리를 만들어간다.
트리에서 가장 가까운 좌표들을 찾는데, 트리는 포함되는 모든 좌표를 의미한다.

공간 복잡도 : O(N^2), 근접 매트릭스를 사용해야하기 때문에 (좌표) N 제곱의 공간이 필요하다.
시간 복잡도 : O(N^3), 가까운 메트릭스를 만드는데 N의 과정들이 필요하며 새로운 좌표들을 찾아 업데이트할때 N^2이 필요하다.
* 명확한 조건을 만들어준다면 N^2log(n)의 시간복잡도까지 줄일 수 있다.

 

계층적 클러스터링의 문제점과 한계

일단 클러스터링을 해버리면 다시 되돌릴 수 없는 문제가 있다.
개체로써의 함수는 지역적으로 최적화 되어있다. 
다른 의미의 데이터들을 사용하면 잡음이나 이상치에 민감해지며, 볼록한 모양이나 크기가 상이한 클러스터들을 다루기 어렵다.
또한 큰 클러스터들을 방해한다.