Maximum Likelihood Estimate : 최대 우도법
모수적인 데이터 밀도 추정 방법으로,
파라미터 (쎄타)로 구성된 하나의 확률밀도함수를 이용한다.
그 확률밀도함에서 관측된 표본 데이터 집합을 On 이라 할때,
이 표본들에서 모수를 추정하는 방법이다.
어떤 모수가 주어졌을 때, 원하는 값들이 나올 가능도를 최대로 만드는 모수를 선택해야한다.

Likelihood Fuction
데이터 샘플에서 후보 분포에 대한 높이 (확률 밀도값 P(~))을 계산해서 모두 곱하여 사용한다.
이를 통해, 지금 얻은 데이터가 해당 분포로부터 나왔을 가능도를 계산할 수 있다.
P(Oi | 쎄타)가 높이라고 볼 수 있다.

Log-likelihood Function
보통은 Log-likelihood Function을 Likelihood Function을 대신하여 많이 사용한다.
Likelihood Function에 Log를 씌워 사용한다.
Maximum Log-likelihood
Log를 씌운 Likelihood Function의 최대값을 찾는다.
argmax는 최대값을 의미한다.
최대값을 구하는 방법은 미분 혹은 편미분을 이용하여, 미분 값이 0이 될때의 값을 찾으면 된다.

Example - Coin | Maximum Likelihood Estimate 예제
- 동전을 던졌을때, 앞 뒤가 각각 나올 확률은 1/2 즉, 0.5 이다.
앞면이 나왔을때를 쎄타로 두고, 뒷면이 나왔을때를 1 - 쎄타로 뒀을때 세타를 구해야한다.

- 동전을 m 번 던졌을때, 각각의 데이터들을 모은것을 D라고 하자.
- 던진 횟수 중에, n번이 앞면이 나온 관점이라고 했을때, 쎼타는 n/m 이다.

- 예를 들어 아래와 같이, 앞, 뒤, 뒤, ... 앞이 나왔다고 했을때,
- 쎄타 x ( 1 - 쎄타 ) x ( 1 - 쎄타 ) ... x 쎄타로 식을 세울 수 있다.
- 그리고 이 식을, m! / n! x ( m - n )! x 쎄타^n x (1 - n)^(m - n) ... 으로 만든다.
- 이 식은 Likelihood Estimation 식이며, 이제 Log를 씌운다.

- Log-likelihood Function은 아래처럼 완성된다.
- 이후, 미분한 값이 0이 됬을때 최대 우도법에 의한 최대값을 찾을 수 있다.
- 여기서 세타는 앞면이 나올 확률, 1 - 쎄타는 뒷면이 나올 확률이다.
- n은 앞면이 나온 관점을 뜻하며 m은 동전을 던진 모든 횟수를 의미한다.

- 이제, 세타 미분 식을 보자.
- 세번째, 식을 보면 미분한 세타값은 n/m 이 된다.


Maximum Likelihood Estimation for Gaussian Distribution :
평균과 분산의 값을 모르는 정규분포에서 o1, o2 ... om 의 값을 모았을때, 이 값들을 이용하여 원래 분포의 평균과 분산을 추축한다. 이 때 구해야하는 모수 쎄타는 (평균, 표준편차) 이다.
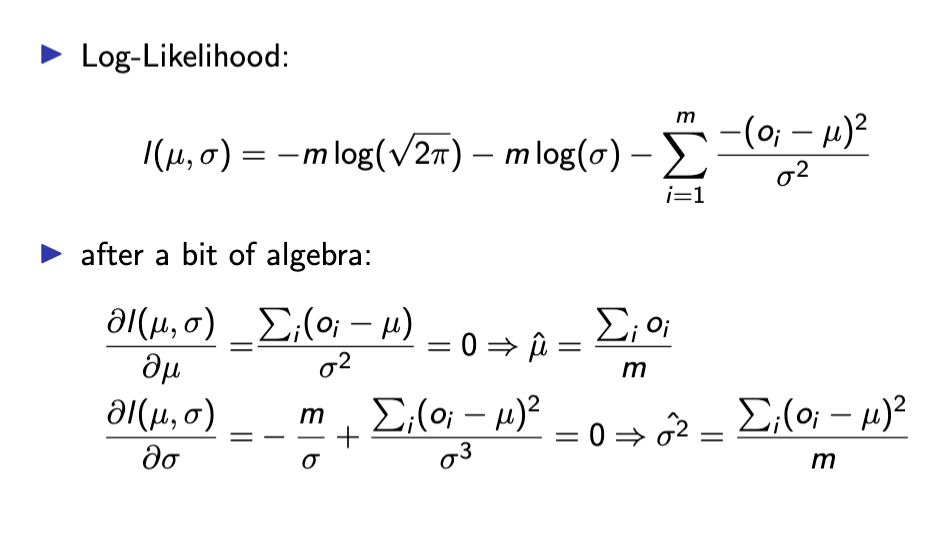
Maximum Likelihood Estimates for Bayesian Networks
- 베이지안 네트워크에도 최대우도법을 적용할 수 있다.


Bayesian Parameter Learning


Bayesian Parameter Learning 예제


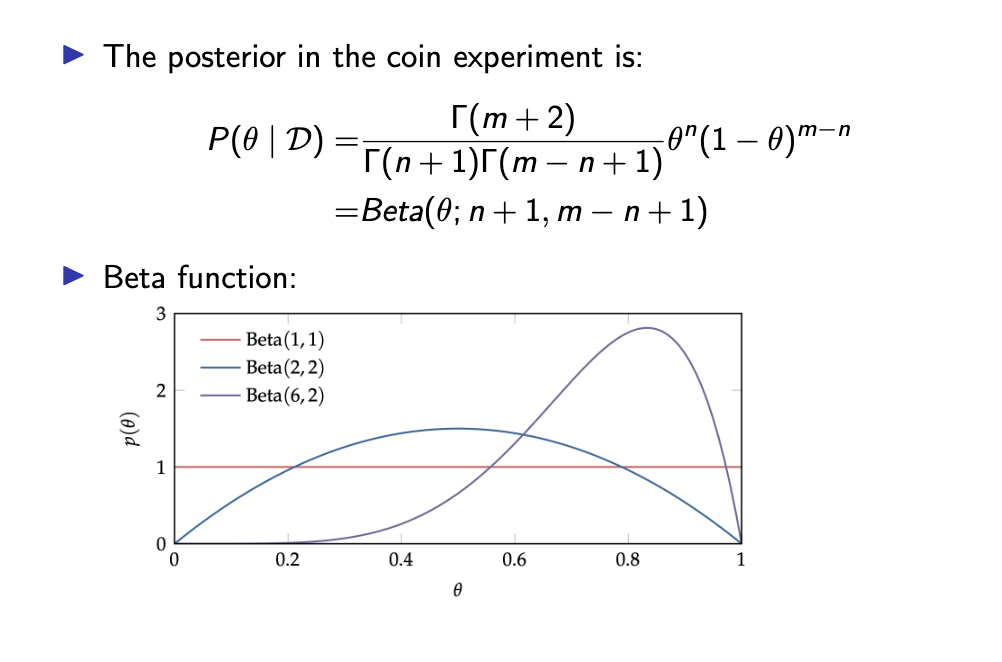
Beta Prior > Beta Posterior

'AI Master Degree > AI and Data engineering' 카테고리의 다른 글
| Chap 5. Decision Making 의사결정 - Policy and Value Iteration Part2. (0) | 2021.10.03 |
|---|---|
| Chap 5. Decision Making 의사결정 - Policy and Value Iteration Part1. (0) | 2021.10.03 |
| Chap 5. Decision Making 의사결정 (0) | 2021.10.02 |
| Chap 4. Parameter learning & Introduction to Simple Decision Making (0) | 2021.09.30 |
