![[Machine Learning] Bias-Variance Tradeoff](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FzRGRU%2FbtrM642AJyQ%2FBCJVQbpmnvt4G678MHMOLk%2Fimg.png)
Bias 란?
- 편향이라고 부르며, Model Prediction 평균과 Ground Truth 사이의 에러를 뜻한다.
- Estimated Function 의 Bias 는 값들을 예측할 수 있는 근본적인 모델의 용량을 알려준다.
Ground Truth 란?
- 학습하고자 하는 데이터의 원본 혹은 실제 값이며, 우리의 모델이 원하는 답으로 예측해주길 바라는 이상적인 데이터를 뜻한다.
Variance 란?
- 한국말로 분산이라고 하며, 주어진 데이터 셋을 위한 모델 예측안의 평균 Variability 이다.
- Variability 는 가변적인 상태 또는 특성이라고 할 수 있다.
- Estimated function 의 Variance 는 함수가 데이터 셋 안에서 얼마나 많이 변화를 조절할 수 있는 가를 말해준다.
Bias 가 높은 경우
- Overly-simplified Model: 너무 단순해진 모델을 의미한다.
- Under-fitting: 모델이 학습 오류를 줄이지 못하게 되는 상황이다.
- High Error on both test and train data: 테스트와 훈련 데이터 모두 에러가 높다.
Variance 가 높은 경우
- Overly-complex Model: 너무 복잡해진 모델을 의미한다.
- Over-fitting: 모델 학습의 오류가 테스트 데이터의 오류보다 훨씬 작은 경우이다.
- Low error on train data and high on test: 테스트에서는 에러가 높고 훈련 데이터에서는 에러가 낮다.
- Starts modelling the noise in the input: 잡음이 많은 인풋에서 모델링을 시작한다.
Under VS Overfitting
Machine Learning 모델은 과거의 경험들로 훈련을 하여, 없는 데이터로 결과를 예측해야한다. ML 모델의 Capacity는 너무 작거나 너무 크지 않아야하며 두가지 상황모두 목표생성에 도움이 되지 않는다.
위 그림에서 가운데 Good Fit/Robust 모델은 좋은 예측 결과를 생산할 것이다.
Underfitting
첫번째 그래프는 Underfitting, 이는 점들은 직선을 이루지 않는다. 아래 다이어그램을 보면 모델이 원으로 제한되어 있다. 즉, 분류되는 결과가 다이어그램의 원 모양을 경계로 분류되는 것 이상으로 좋아질 수 없다.
위에서 설명한 것처럼, Underfitting 은 모델이 훈련을 할때 선택할 수 있는 Features 이 매우 적거나 모델을 다룰 리소스가 충분하지 않음을 나타낸다. 또한 Underfitting 은 High Bias and Low Variance 라고도 불린다.
High Bias 는 모델의 Solution 을 선형으로 만들어지는 것을 추구하게 된다.
Low Variance 는 Features 의 가변성을 제한시키는 것을 추구하게 된다.
해결책
- Non-linear 그리고 복잡한 모델들을 사용하자
- Layer 들의 갯수 그리고, 또는 Neural Networks 의 유닛들의 갯수를 증가시키자
- 더 많은 Features 을 추가하자
- 이미 존재하는 리소스들을 사용하여 더 많이 복잡한 Features 을 다루자
Overfitting
과적합 Overfitting 은 모델이 과하게 훈련 됬을때, 창의적인 모델이 되는 것과 훈련에 최적화 된 모델이다.
하지만 Overfitting 은 실제 테스트 데이터에서는 좋은 예측 결과나 성능을 발휘하지 못한다.
또한, Overfitting 은 Low Bias and High Variance 라고도 부른다. Bias 가 낮으면 특정한 선형 linear 혹은 다형 polynomial 인 솔루션을 생성한다. 이 모델은 큰 분산 Variance 를 가지고 어떤 functions 혹은 어떠한 것도 고려하게 된다. 두가지 특징들은 전체적인 모델 예측 에러가 상승하는 것에 기여할 것이다.
예제: 고양이 사진이 아니어도 Overfitting 된 모델은 고양이 모양을 창조할 것이다.
Underfitting, Overfitting 학습 프로세스를 모니터하는 방법
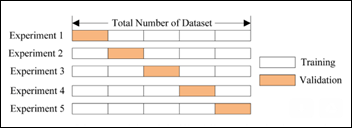
일반적인 훈련과 테스트는 80:20 비율로, 데이터가 랜덤하게 선택되어 진행된다. 이는 전체 데이터 세트와 모델이 알지 말아야하는 것, 치팅하는 것과 같은 방식으로의 모델 결정을 만드는 것에 영향을 끼치는 표준 편차와 평균을 학습하는 것, 그리고 전체 데이터 세트에 정규화하는 시나리오를 쉽게 막을 수 있다.
또한 트레이닝 데이터를 다른 하이퍼 파라미터나 구조 등에 여러번 모델에 노출시켜 학습을 시켜 모델이 모든 데이터를 기억하는 것을 막을 수 있다. 위 그림 처럼 Cross-Validation Scheme 을 이용하여 같은 트레이닝 데이터 세트를 각각 훈련 Epoch 에 검증할 수 있다. 20% 의 테스트 데이터를 미니 세트로 만들어 각 훈련 Epoch 마다 훈련을 진행하여 과적합, 과소적합을 조절할 수 있다.
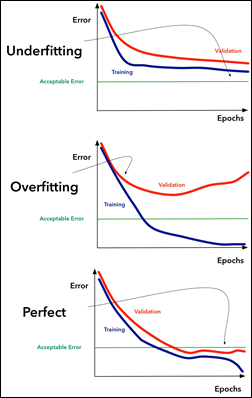
Error with Epoch, Learning Curve
Underfitting Error and Epochs 그래프를 보면 오류 값이 허용 가능한 에러 임계값 Acceptable Error 이상으로 남아 있는 것을 볼 수 있다. 즉 모델은 학습을 하지 않는다.
- 모델 용량 늘리기 Increase Model Cabacity
- 복잡성과 특징들 각각 늘리거나 모두 늘리기 Increase the number of features or complexity, or both
- 훈련 샘플 추가 Add more training samples
Overfitting 그래프에서는 Validation 선과 Training 선이 분리 될때 Overfitting 이 시작 되는 것을 보여준다. 훈련 곡선은 계속해서 에러를 낮추지만 검증 곡선은 에러가 줄어들다가 어느 순간 다시 증가한다.
- 모델의 용량 낮추기 Decrease the model capacity
- 특징 낮추기 Decrease the number of features
- 샘플 늘리기 Increase the number of samples
Perfect 한 그래프는 검증 곡선이 허용 가능한 에러 임계값 미만을 유지하고 훈련 곡선에서 분리 되기 시작한다.
이때는 훈련을 멈춰야한다.
학습 률 Learning Rate
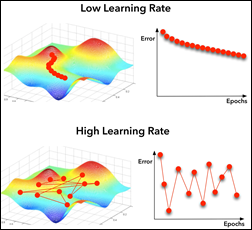
Machine Learning 모델은 파라미터들을 가진다. 예를 들어 Weights 가중치. 그리고 학습률과 같은 Hyper-parameters 를 가지고 있다. 위의 그래프들의 목표는 최적의 cost function 을 찾는 것이 목표이다.
학습률이 너무 높다면, 학습할 때마다 아주 큰 도약을 하기 때문에 모델이 전역 최소값 Global Minimum 을 놓칠 것이다. 반대로 학습률이 너무 낮다면 전역 최소값을 찾는데 시간이 너무 걸린다.
데이터 증가 Data Augmentation
강아지와 고양이를 식별하는 것과 같은 이미지 식별 모델을 고려했을때, 일반적으로 과적합 모델을 제공하기 위해 더 많은 샘플들을 수집하는 것은 시간, 비용 및 리소스를 소모하는 활동이다. 이를 위해 모델이 과적합 되기 시작할 때까지 모델 용량을 점진적으로 늘린다.
그 후, 훈련 세트에서만 사용되는 Data Augmentation 을 추가하는 것이 일반적이다. 아래와 같은 이미지 매개변수들을 중심으로 랜덤으로 데이터가 다시 선택된다.
- Zoom
- Scale
- Brightness
- Skew
- Mirror around vertical/horizontal axes
- Colors
Regularizers
과적합을 처리하기 위한 방법 중의 하나이다. Hyper-parameter 인 Regularizer 를 사용하여 모델 가중치를 수정하지 않고 훈련을 진행하면 모델이 결론으로 바로 뛰어들지 않는다.
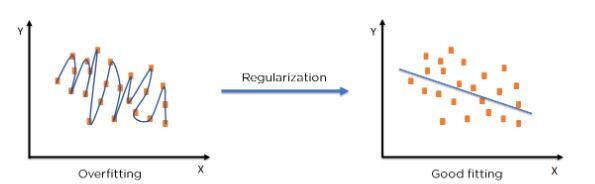
모델의 손실 함수 Loss function 을 최소화하고 Overfitting, Underfitting 을 방지하기 위해 사용되는 보정 기술이다. 위 그림처럼 정규화를 통해 테스트 세트에 모델을 적절하게 맞춰 오류를 줄 일 수 있다. 대표적으로 두가지 Regularization 기술이 있다.
- Ridge Regularization
- Penalty equivalent 를 Coefficients 의 제곱의 합에 더하여 사용한다.
- Coefficients 를 최소하는 것이 목적이다.
- Cost function 에서 Lambda λ 는 페널티를 의미하며, 이 값을 증가시키면 Coefficients 값이 감소한다.
- Multicollinearity 를 막기위해 사용되며, 모델의 복잡도를 감소시킨다.
- Lasso Regression
- Coefficient 절대값의 합에 Penalty equivalent 를 곱한 값을 추가하여 model 을 수정한다.
- Coefficient 최소화가 목표이다.
Covariance and Correlation
Covariance 공분산은 평균에서 한 변수 X 의 편차가 다른 변수 Y 의 편차와 관련된 정도의 양적 측정이다. 즉 두 확률 변수가 서로 나란히 증가하거나 감소하는 정도, 어떻게 두 변수가 함께 변화하는지를 나타낸다.
- 두 확률 변수가 나란히 변하는 정도를 나타낸다.
- Covariance 는 Coefficient 의 척도이다.
- 변수간의 선형 관계의 방향을 나타낸다.
- -∞와 +∞ 사이에서 달라질 수 있다.
- 규모의 변화에 영향을 받는다.
- 두 변수의 단위 곱에서 단위를 가정한다.
- 평균적으로 실제 양(cm, kg) 가 공변하는 정도를 측정한다.
- 독립 변수의 경우 Covariance 는 0 이다. (한 변수가 움직이고 다른 변수는 움직이지 않음, 반드시 변수들이 함께 움직이지 않기 때문)
Correlation 상관관계는 이 관계의 강도와 방향을 모두 알려준다. 다양한 변수의 변화가 서로 관련되어 있는지 여부와 얼마나 강하게 관련되어 있는지 결절하는데 도움이 된다.
- 두 확률 변수가 서로 얼마나 강하게 관련되어 있는지를 나타낸다.
- Covarinace 의 척도화된 형태이다.
- 선형 관계의 강도와 방향을 모두 측정한다.
- -1 과 +1 사이의 상관 관계 범위
- 규모의 영향을 받지 않는다.
- 무차원이라 변수 간의 관계에는 단위가 없다.
- 평균적으로 얼마나 변하는지에 대한 비율을 측정한다.
- 완전히 독립된 변수는 상관관계가 0이다.
Dropout
훈련 세트에서만 사용되며, 무시할 뉴런들을 랜덤으로 선택하는 기법이다. 뉴런은 특정 Feature 에 맞게 조정되어 전문화가 될 수 가 있는데, 이러한 문제가 커지면 특정 상황에 특화된 취약한 모델이 될 수 있다. 만약 뉴런이 훈련 중에 랜덤으로 무시된다면 다른 뉴런이 개입하여 그 부분을 예측할 것이다. 이를 Complex co-adpatations 이라고 부른다.
결국, Dropout 을 사용하여 네트워크가 뉴런의 특정 가중치에 덜 민감하도록 조절할 수 있다. 결과적으로 네트워크를 더 나은 일반화로 이끌게 되고 Overfitting 의 가능성을 줄여준다.
Bias Variance Trade-off
- 편향 Bias 가 증가하면 Variance 가 줄어든다 (항상 그렇지는 않다)
- Error = bias^2 + variance +irreducible error
- 모델이 너무 단순하고 Parameters 가 매우 적을때 Bias 는 높고 Variances 는 낮을 수 있다.
- 모델에 많은 수의 Parameters 가 존재하면 높은 Variance 와 낮은 Bias 를 갖게 된다.
좋은 모델을 만들기 위해서는 전체 오류를 최소화 하도록 Bias 와 Variance 사이의 적절한 균형을 찾아야 한다.
'컴퓨터공학 > Machine Learning Study' 카테고리의 다른 글
| Imbalanced Data in Classification, 분류에서 불안정한 데이터 (0) | 2022.10.26 |
|---|---|
| P-value란? 유의 확률 (0) | 2022.10.26 |
| [머신러닝 시스템 디자인 스터디 Part5] Performance and Capacity Considerations (0) | 2022.08.18 |
| [머신러닝 시스템 디자인 스터디 Part5]Offline model building and evaluation (0) | 2022.08.14 |
| [머신러닝 시스템 디자인 스터디 Part4]Architecting for Scale (0) | 2022.08.12 |