323. Number of Connected Components in an Undirected Graph
Medium
You have a graph of n nodes. You are given an integer n and an array edges where edges[i] = [ai, bi] indicates that there is an edge between ai and bi in the graph.
Return the number of connected components in the graph.
Example 1:
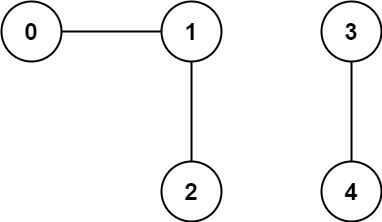
Input: n = 5, edges = [[0,1],[1,2],[3,4]]
Output: 2
Example 2:

Input: n = 5, edges = [[0,1],[1,2],[2,3],[3,4]]
Output: 1
Constraints:
- 1 <= n <= 2000
- 1 <= edges.length <= 5000
- edges[i].length == 2
- 0 <= ai <= bi < n
- ai != bi
- There are no repeated edges.
문제 풀이
- 노드의 개수와 간선들의 정보가 주어진다.
- 간선들의 정보를 이용하여 연결되어 있는 그룹의 개수를 구해야한다.
- 간선들은 방향을 갖지 않기 때문에 a에서 b로 b에서 a로 이동할 수도 있다.
- 만약 간선이 없는 노드라면 그 노드는 다른 그룹이다.
- 양방향 간선들을 딕셔너리로 만든다.
- 재귀함수를 사용하여 0부터 n-1 까지 탐색해야한다.
- 만일 간선이 없다면 정답 그룹 개수를 1개 늘리고, 간선이 존재한다면 재귀함수를 이용하여 탐색해야한다.
- 탐색하면서 이미 방문한 노드는 visited 배열로 처리해주자.
참고로, Union-Find를 활용하여 그룹의 개수를 구하는 방법도 있지만 생략한다.
소스 코드
class Solution:
def countComponents(self, n: int, edges: List[List[int]]) -> int:
cnt = 0
visited = [0] * (n + 1)
mp = defaultdict(list)
for y, x in edges:
mp[y].append(x)
mp[x].append(y)
def rec(num):
for x in mp[num]:
if visited[x] == 1: continue
visited[x] = 1
rec(x)
for i in range(0, n):
if i not in mp:
cnt += 1
continue
if visited[i] == 1: continue
visited[i] = 1
rec(i)
cnt += 1
return cnt'컴퓨터공학 > LeetCode 1000' 카테고리의 다른 글
| [LeetCode] 739. Daily Temperatures (0) | 2022.12.20 |
|---|---|
| [LeetCode] 2272. Substring With Largest Variance (0) | 2022.12.09 |
| [LeetCode] 2256. Minimum Average Difference (0) | 2022.12.07 |
| [LeetCode] 328. Odd Even Linked List (0) | 2022.12.07 |
| [LeetCode] 1165. Single-Row Keyboard (0) | 2022.12.02 |
![[LeetCode] 323. Number of Connected Components in an Undirected Graph](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FQAK4h%2FbtrS5xkuAtL%2FAAAAAAAAAAAAAAAAAAAAACOGGc0Z74zCPGoa_F4C4_KqAv7mFQrNeBjylPcdIQqu%2Fimg.jpg%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3D60wZEbnQJuFPoSIn%252BuN99Ottr2M%253D)